【理論】令和5年 (下期) 問15|三相交流回路におけるY結線およびΔ結線負荷の電流・電力計算問題
抵抗 \( R \) [\(\( \Omega \)\)],誘導性リアクタンス \( X \) [\(\( \Omega \)\)] からなる平衡三相負荷(力率 \( 80 \) [%])に対称三相交流電源を接続した交流回路がある。
次の (a) および (b) の問いに答えよ。
図1のように,\( \mathrm{Y} \) 結線した平衡三相負荷に線間電圧 \( 210 \) [V] の三相電圧を加えたとき,回路を流れる線電流 \( I \) は \( \displaystyle \frac{14}{\sqrt{3}} \) [A] であった。
負荷の誘導性リアクタンス \( X \) の値 [\( \Omega \)] として,最も近いものを次の (1)~(5) のうちから一つ選べ。
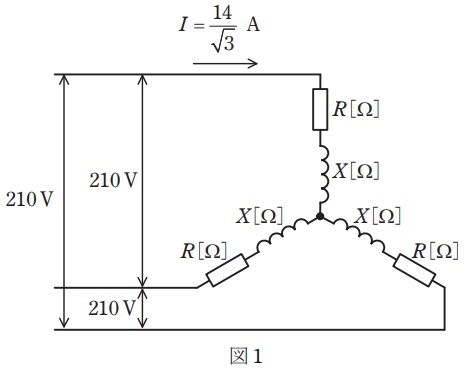
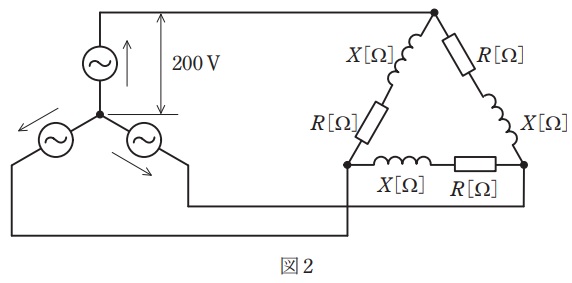
(b) 図1の各相の負荷を使って \( \Delta \) 結線し,図2のように相電圧 \( 200 \) [V] の対称三相電源に接続した。
この平衡三相負荷の全消費電力の値 [\( \mathrm{kW} \)] として,最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
三相交流回路の基本原理
三相交流は、位相が120°ずつずれた3つの正弦波電圧・電流からなる電力システムです。日本の電力系統では50Hz(東日本)または60Hz(西日本)の三相交流が使用されています。
三相交流の特徴
- 電力の脈動がなく、一定の出力が得られる
- 同じ電力を送る場合、単相よりも導体が細くて済む
- 三相誘導電動機などの回転機に適している
- 三相平衡時は中性線に電流が流れない
三相交流回路の結線方式には主に2種類あります:
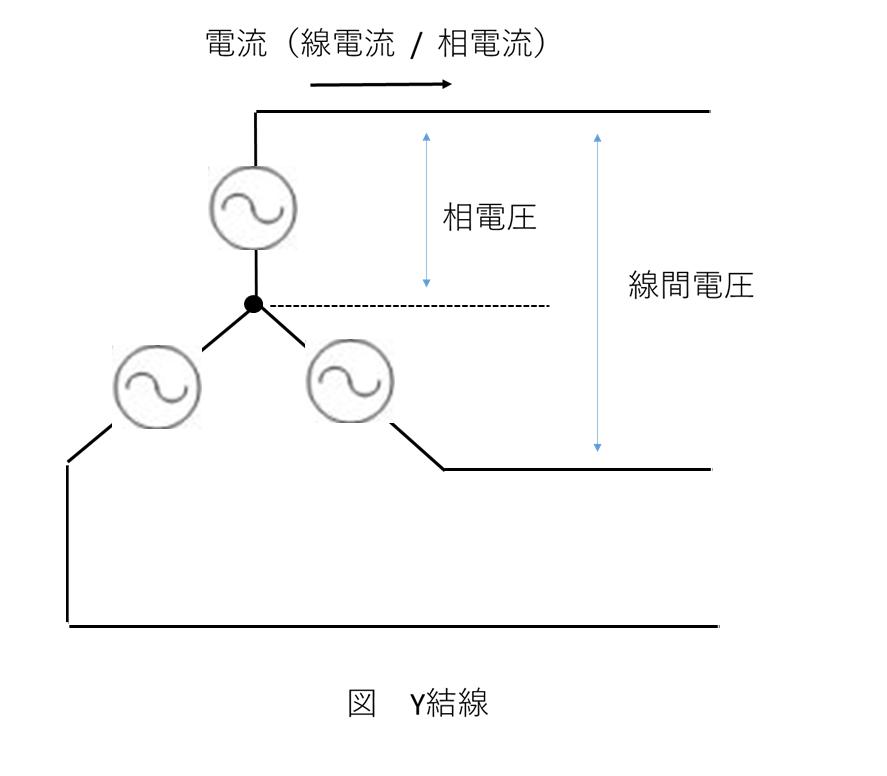
Y結線(スター結線)
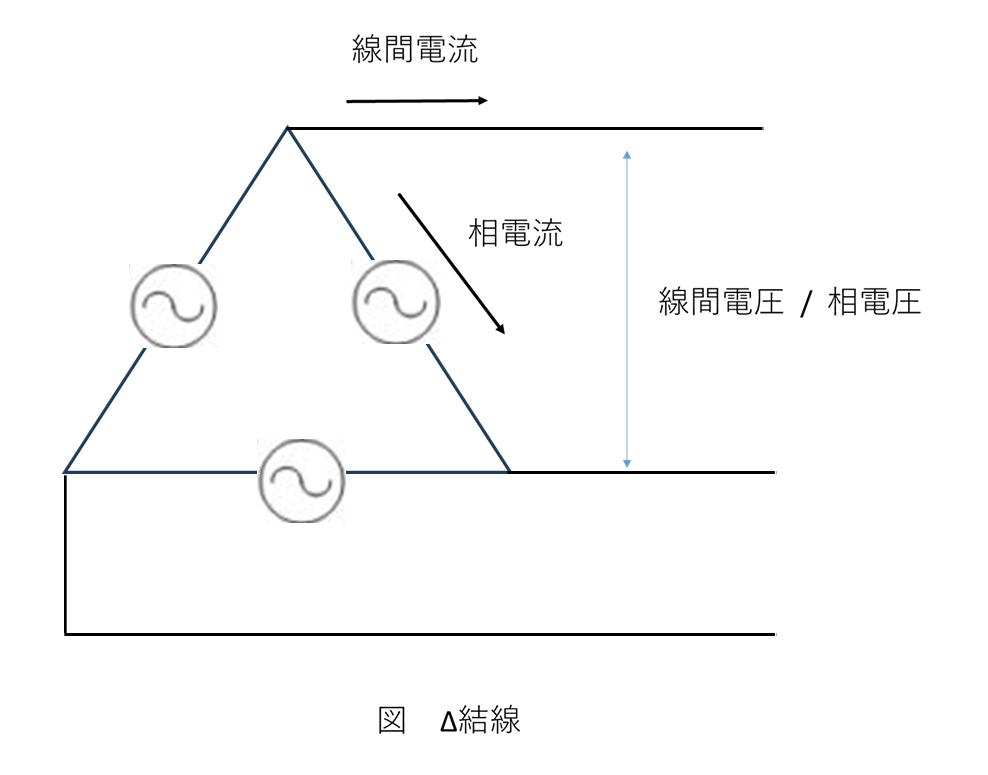
Δ結線(デルタ結線)
Y結線の特徴
- 各相の一端が共通点(中性点)で接続される
- 線間電圧は相電圧の√3倍
- 線電流と相電流は等しい
- 中性点が利用できる
Δ結線の特徴
- 各相が環状に接続される
- 線間電圧と相電圧は等しい
- 線電流は相電流の√3倍
- 一相が故障しても運転可能
三相平衡回路(各相の負荷が等しい場合)では、計算を簡略化するために一相分の等価回路で考えることができます。
電圧・電流の関係
1. 回路素子のインピーダンスと電圧・電流の関係
抵抗、コイル、コンデンサのインピーダンスは次のように表されます:
\[ \begin{aligned} \dot{Z}_{\mathrm{R}} &= R \\[10pt] \dot{Z}_{\mathrm{L}} &= \mathrm{j}\omega L = \mathrm{j}2\pi f L \\[10pt] \dot{Z}_{\mathrm{C}} &= \frac{1}{\mathrm{j}\omega C} = \frac{1}{\mathrm{j}2\pi f C} \\[10pt] \end{aligned} \]
それぞれの電圧と電流の関係は:
\[ \begin{aligned} \dot{V}_{\mathrm{R}} &= R\dot{I} \\[10pt] \dot{V}_{\mathrm{L}} &= \mathrm{j}\omega L \dot{I} \\[10pt] \dot{V}_{\mathrm{C}} &= \frac{\dot{I}}{\mathrm{j}\omega C} \\[10pt] \end{aligned} \]
2. Y結線における電圧関係
Y結線では、線間電圧の大きさは相電圧の√3倍であり、相電圧より30°進みます:
\[ \begin{aligned} V_{\mathrm{ab}} &= \sqrt{3}E_{\mathrm{a}} \\[10pt] V_{\mathrm{bc}} &= \sqrt{3}E_{\mathrm{b}} \\[10pt] V_{\mathrm{ca}} &= \sqrt{3}E_{\mathrm{c}} \\[10pt] \end{aligned} \]
Y結線の電圧ベクトル図
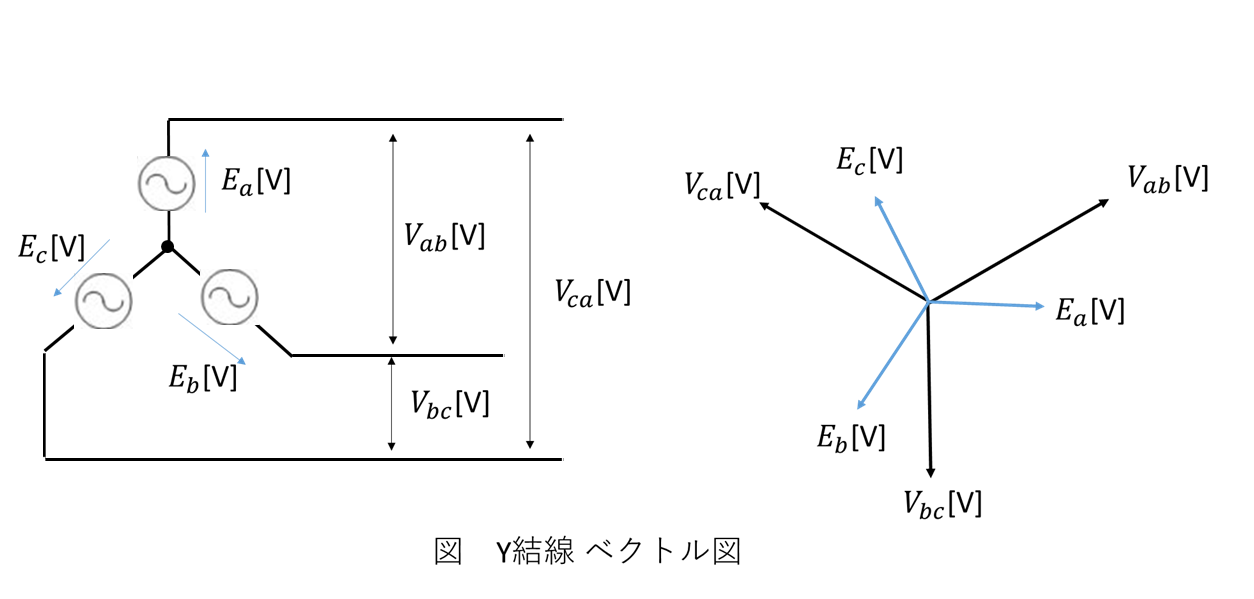
線間電圧は相電圧に対して30°進みであることに注意
3. Δ結線における電流関係
Δ結線では、線電流の大きさは相電流の√3倍であり、相電流より30°遅れます:
\[ \begin{aligned} I_{\mathrm{a}} &= \sqrt{3}I_{\mathrm{ab}} \\[10pt] I_{\mathrm{b}} &= \sqrt{3}I_{\mathrm{bc}} \\[10pt] I_{\mathrm{c}} &= \sqrt{3}I_{\mathrm{ca}} \\[10pt] \end{aligned} \]
Δ結線の電流ベクトル図
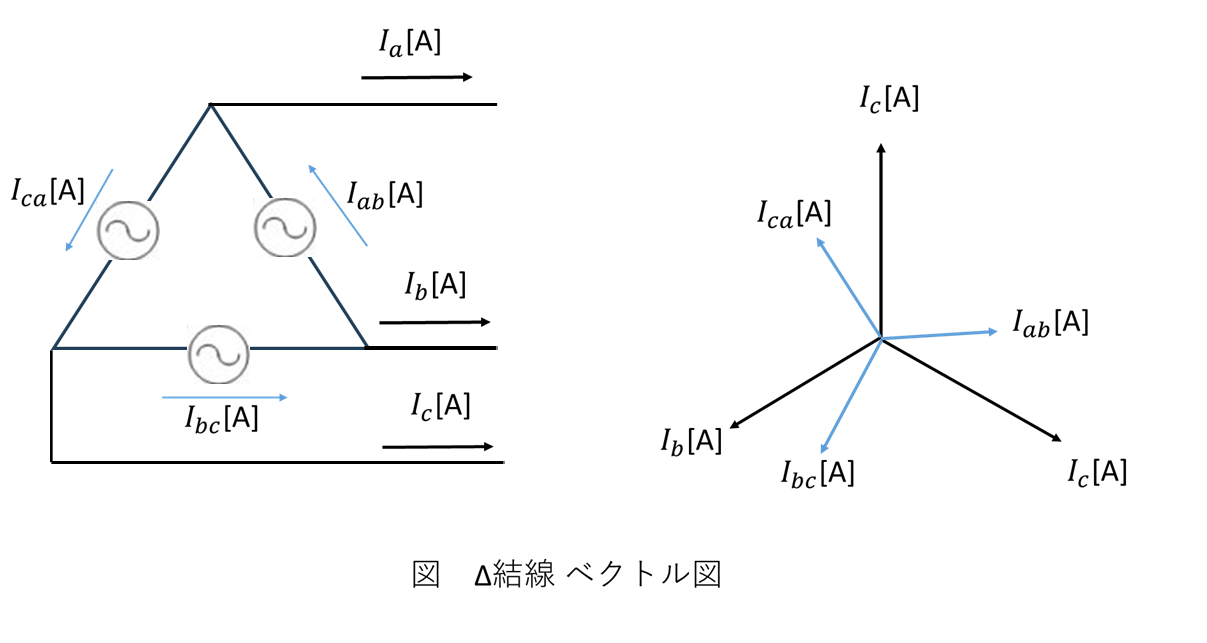
線電流は相電流に対して30°遅れであることに注意
例題:Y結線の電圧計算
三相平衡Y結線において、相電圧が100V(実効値)のとき、線間電圧を求めなさい。
解答
Y結線では線間電圧は相電圧の√3倍なので:
\(V_{\mathrm{線間}} = \sqrt{3} \times V_{\mathrm{相}} = \sqrt{3} \times 100 = 173.2\) [V]
電力計算
1. 電力の種類と関係
- 有効電力 \(P\) [W]:抵抗で消費される実際に使える電力
- 無効電力 \(Q\) [var]:リアクタンスで消費・供給される電力
- 皮相電力 \(S\) [VA]:有効電力と無効電力のベクトル和
これらの関係は以下の式で表されます:
\[ \begin{aligned} S &= \sqrt{P^2 + Q^2} \\[10pt] \cos\theta &= \frac{P}{S} \\[10pt] \end{aligned} \]
ここで \(\cos\theta\) は力率を表します。
電力のベクトル図
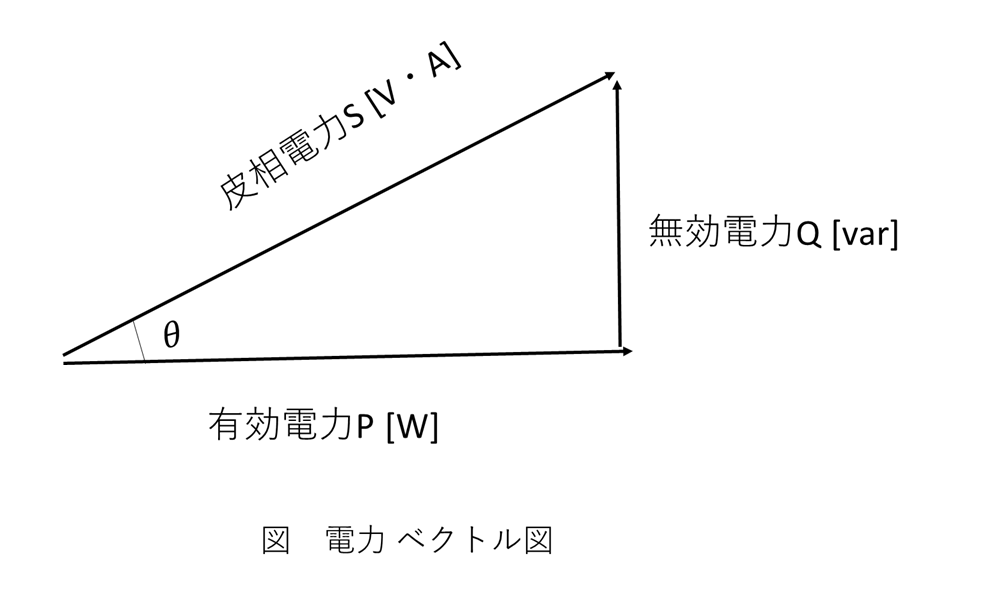
有効電力P、無効電力Q、皮相電力Sの関係
2. 電流と電力の関係
線路に電流 \(I\) [A] が流れているとき、インピーダンス \(Z\) [Ω]、抵抗 \(R\) [Ω]、リアクタンス \(X\) [Ω] を用いて電力は次のように表されます:
\[ \begin{aligned} S &= ZI^2 \\[10pt] P &= RI^2 \\[10pt] Q &= XI^2 \\[10pt] \end{aligned} \]
インピーダンスのベクトル図
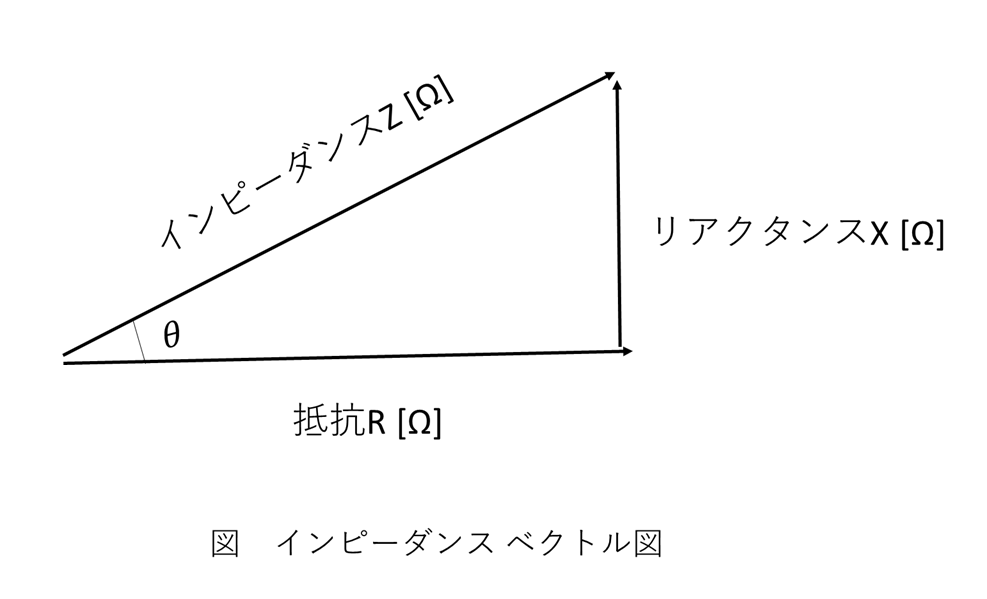
インピーダンスZ、抵抗R、リアクタンスXの関係
3. 三相回路の全電力
三相平衡回路の全電力は一相あたりの電力の3倍です:
\[ \begin{aligned} P_{\mathrm{三相}} &= 3P_{\mathrm{一相}} = 3V_{\mathrm{相}}I_{\mathrm{相}}\cos\theta \\[10pt] \end{aligned} \]
これを線間電圧 \(V_{\mathrm{線間}}\) と線電流 \(I_{\mathrm{線}}\) で表すと:
Y結線の場合
\[ \begin{aligned} P_{\mathrm{三相}} &= \sqrt{3}V_{\mathrm{線間}}I_{\mathrm{線}}\cos\theta \\[10pt] \end{aligned} \]
Δ結線の場合
\[ \begin{aligned} P_{\mathrm{三相}} &= \sqrt{3}V_{\mathrm{線間}}I_{\mathrm{線}}\cos\theta \\[10pt] \end{aligned} \]
Y結線とΔ結線の式が同じ形になることに注意してください。これは三相平衡状態ではどちらの結線でも同じ電力を扱えることを示しています。
例題:三相回路の電力計算
三相平衡回路において、線間電圧が200V、線電流が10A、力率が0.8のとき、三相全体の有効電力を求めなさい。
解答
\[ \begin{aligned} P_{\mathrm{三相}} &= \sqrt{3} \times V_{\mathrm{線間}} \times I_{\mathrm{線}} \times \cos\theta \\[10pt] &= \sqrt{3} \times 200 \times 10 \times 0.8 \\[10pt] &= 2771\ \mathrm{[W]} \end{aligned} \]
Δ-Y変換
Δ結線とY結線の変換
回路の計算を簡略化するために、Δ結線とY結線の間で変換を行うことがあります。
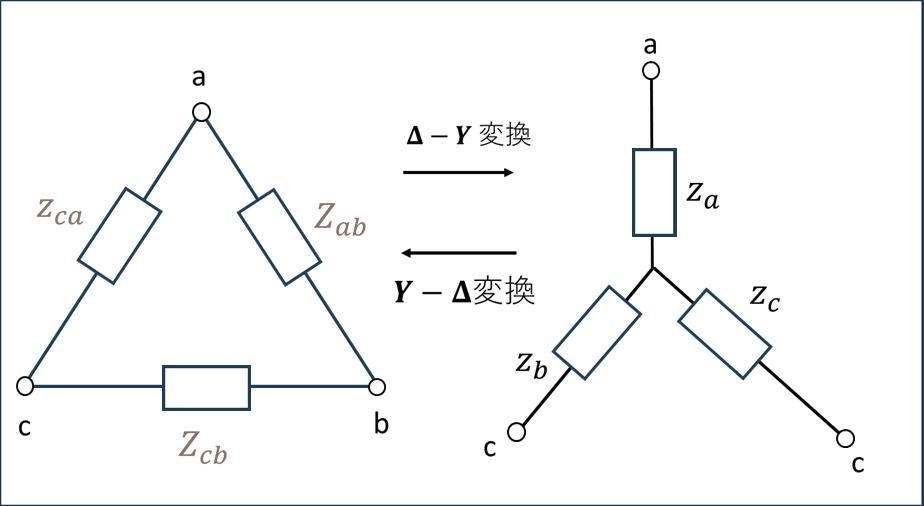
1. Δ→Y変換の公式
\[ \begin{aligned} \dot{Z}_{\mathrm{a}} &= \frac{\dot{Z}_{\mathrm{ab}}\dot{Z}_{\mathrm{ca}}}{\dot{Z}_{\mathrm{ab}}+\dot{Z}_{\mathrm{bc}}+\dot{Z}_{\mathrm{ca}}} \\[10pt] \dot{Z}_{\mathrm{b}} &= \frac{\dot{Z}_{\mathrm{bc}}\dot{Z}_{\mathrm{ab}}}{\dot{Z}_{\mathrm{ab}}+\dot{Z}_{\mathrm{bc}}+\dot{Z}_{\mathrm{ca}}} \\[10pt] \dot{Z}_{\mathrm{c}} &= \frac{\dot{Z}_{\mathrm{ca}}\dot{Z}_{\mathrm{bc}}}{\dot{Z}_{\mathrm{ab}}+\dot{Z}_{\mathrm{bc}}+\dot{Z}_{\mathrm{ca}}} \\[10pt] \end{aligned} \]
2. Y→Δ変換の公式
\[ \begin{aligned} \dot{Z}_{\mathrm{ab}} &= \frac{\dot{Z}_{\mathrm{a}}\dot{Z}_{\mathrm{b}}+\dot{Z}_{\mathrm{b}}\dot{Z}_{\mathrm{c}}+\dot{Z}_{\mathrm{c}}\dot{Z}_{\mathrm{a}}}{\dot{Z}_{\mathrm{c}}} \\[10pt] \dot{Z}_{\mathrm{bc}} &= \frac{\dot{Z}_{\mathrm{a}}\dot{Z}_{\mathrm{b}}+\dot{Z}_{\mathrm{b}}\dot{Z}_{\mathrm{c}}+\dot{Z}_{\mathrm{c}}\dot{Z}_{\mathrm{a}}}{\dot{Z}_{\mathrm{a}}} \\[10pt] \dot{Z}_{\mathrm{ca}} &= \frac{\dot{Z}_{\mathrm{a}}\dot{Z}_{\mathrm{b}}+\dot{Z}_{\mathrm{b}}\dot{Z}_{\mathrm{c}}+\dot{Z}_{\mathrm{c}}\dot{Z}_{\mathrm{a}}}{\dot{Z}_{\mathrm{b}}} \\[10pt] \end{aligned} \]
平衡三相回路での簡略化
平衡三相回路(\(\dot{Z}_{\mathrm{ab}} = \dot{Z}_{\mathrm{bc}} = \dot{Z}_{\mathrm{ca}}\) および \(\dot{Z}_{\mathrm{a}} = \dot{Z}_{\mathrm{b}} = \dot{Z}_{\mathrm{c}}\))では:
\(\dot{Z}_{\mathrm{ab}} = \dot{Z}_{\mathrm{bc}} = \dot{Z}_{\mathrm{ca}} = 3\dot{Z}_{\mathrm{a}} = 3\dot{Z}_{\mathrm{b}} = 3\dot{Z}_{\mathrm{c}}\)
つまり、平衡三相回路では、Δ結線のインピーダンスはY結線のインピーダンスの3倍となります。
例題:Δ-Y変換
平衡Δ結線において、各相のインピーダンスが \(Z_{\mathrm{Δ}} = 30\) [Ω] の場合、等価なY結線の各相のインピーダンスを求めなさい。
解答
平衡三相回路では \(Z_{\mathrm{Y}} = \frac{Z_{\mathrm{Δ}}}{3}\) となるので:
\(Z_{\mathrm{Y}} = \frac{30}{3} = 10\) [Ω]
🔍 ワンポイントアドバイス: 三相交流回路の計算では、「Y結線では線間電圧が相電圧の√3倍で30°進み」「Δ結線では線電流が相電流の√3倍で30°遅れ」という関係を覚えておくことが重要です。また、三相平衡回路では、計算を一相分に簡略化できる点と、三相全電力が \(P_{\mathrm{三相}} = \sqrt{3}V_{\mathrm{線間}}I_{\mathrm{線}}\cos\theta\) で計算できることをマスターしておきましょう。第3種電気主任技術者試験では、Y結線とΔ結線の変換や電力計算に関する問題がよく出題されます。
今日は三相回路の計算をするで!まずはY結線とΔ結線の基本的な特徴から確認していこか。Y結線とΔ結線の違いは何やと思う?
Y結線とΔ結線の違いについて説明します。
Y結線(スター結線)は、三相の巻線や負荷の一端を共通接続点(中性点)で接続し、残りの端子を電源または負荷に接続する方式です。特徴としては相電圧と線間電圧の関係が \(V_{線間} = \sqrt{3} \times V_{相}\) となり、相電流と線電流が等しくなります。
Δ結線(デルタ結線)は、三相の巻線や負荷を三角形状に接続する方式です。特徴としては相電圧と線間電圧が等しく、相電流と線電流の関係が \(I_{線} = \sqrt{3} \times I_{相}\) となります。
ええ説明やな!じゃあ、今日の問題に取り組んでいこか。まずは(a)の問題からや。
図1の回路は三相平衡負荷で、線間電圧210[V]、線電流が14[A]、力率が0.8(遅れ)やって。まずは相電圧を求めてみてくれるか?
相電圧を求めます。Y結線の場合、線間電圧と相電圧の関係は以下の式で表されます:
\( V_{線間} = \sqrt{3} \times V_{相} \)
これを相電圧について解くと:
\( V_{相} = \frac{V_{線間}}{\sqrt{3}} \)
与えられた線間電圧210[V]を代入します:
\[ \begin{eqnarray} V_{相} = E &=& \frac{210}{\sqrt{3}} \ \mathrm{[V]} \\[20pt] &\approx& 121.2 \ \mathrm{[V]} \end{eqnarray} \]したがって、相電圧は約121.2[V]です。
そうやな!Y結線の場合、相電圧は線間電圧を√3で割った値になるんや。次に、負荷のインピーダンスの大きさを求めてみよか。オームの法則を使うとどうなる?
負荷のインピーダンスの大きさをオームの法則で求めます。
Y結線では線電流と相電流が等しいので、インピーダンスは相電圧を相電流で割ることで求められます:
\[ \begin{eqnarray} Z &=& \frac{E}{I} \\[20pt] &=& \frac{\frac{210}{\sqrt{3}}}{\frac{14}{\sqrt{3}}} \\[20pt] &=& \frac{210}{14} \\[20pt] &=& 15 \ \mathrm{[\Omega]} \end{eqnarray} \]したがって、負荷のインピーダンスの大きさは15[Ω]です。
よくできてるな!次に、力率が0.8(遅れ)ということやから、誘導性リアクタンスXを求めてみよか。力率とインピーダンスの関係からどうやって求められる?
誘導性リアクタンスXを求めます。
力率は \( \cos\theta = 0.8 \) なので、インピーダンスの三角形から:
抵抗R = Z·cos θ
リアクタンスX = Z·sin θ
ここで、sin θは三角関数の関係から \( \sin\theta = \sqrt{1-\cos^2\theta} \) で求められます。
\[ \begin{eqnarray} X &=& Z\sin\theta \\[20pt] &=& Z\sqrt{1-\cos^2\theta} \\[20pt] &=& 15 \times \sqrt{1-0.8^2} \\[20pt] &=& 15 \times \sqrt{1-0.64} \\[20pt] &=& 15 \times \sqrt{0.36} \\[20pt] &=& 15 \times 0.6 \\[20pt] &=& 9 \ \mathrm{[\Omega]} \end{eqnarray} \]したがって、誘導性リアクタンスの大きさは9[Ω]です。
これで問題(a)の答えは選択肢の(3)となります。
ええ計算や!これで問題(a)の答えが選択肢(3)の9[Ω]と確認できたな。
次は問題(b)に進むで。まずは抵抗Rの大きさを求めていこか。力率とインピーダンスからどう求められる?
抵抗Rの大きさを計算します。
力率とインピーダンスの関係から:
\[ \begin{eqnarray} R &=& Z\cos\theta \\[20pt] &=& 15 \times 0.8 \\[20pt] &=& 12 \ \mathrm{[\Omega]} \end{eqnarray} \]したがって、抵抗の大きさは12[Ω]です。
そうやな!次に問題の重要なポイントやけど、図2の負荷はΔ結線になってるようやな。これをY結線に変換して計算する必要があるんや。Δ-Y変換の式って覚えてるか?
Δ-Y変換の式は以下のとおりです:
Δ結線からY結線へ変換する場合:
\( Z_Y = \frac{Z_{\Delta}}{3} \)
ここで、Z_Yはスター結線(Y結線)のインピーダンス、Z_Δはデルタ結線(Δ結線)のインピーダンスです。
Y結線からΔ結線へ変換する場合は逆に:
\( Z_{\Delta} = 3Z_Y \)
となります。
ええやん!じゃあ、実際にΔ結線からY結線への変換を行ってみよか。抵抗RとリアクタンスXはどうなる?
Δ結線からY結線への変換を行います。
\[ \begin{eqnarray} R_Y &=& \frac{R}{3} \\[20pt] &=& \frac{12}{3} \\[20pt] &=& 4 \ \mathrm{[\Omega]} \\[20pt] X_Y &=& \frac{X}{3} \\[20pt] &=& \frac{9}{3} \\[20pt] &=& 3 \ \mathrm{[\Omega]} \end{eqnarray} \]したがって、Y結線に変換後の抵抗は4[Ω]、リアクタンスは3[Ω]となります。
計算合ってるで!次に、線路を流れる電流I'を求めてみよか。問題文には相電圧E'=200[V]と書いてあるみたいやけど、これを使ってどう計算する?
線路を流れる電流I'を計算します。
Y結線では線電流と相電流が等しいので、オームの法則を使って計算できます。まず、変換後のY結線のインピーダンスの大きさを求めます:
\[ \begin{aligned} Z_Y &= \sqrt{R_Y^2 + X_Y^2} \\[10pt] &= \sqrt{4^2 + 3^2} \\[10pt] &= \sqrt{16 + 9} \\[10pt] &= \sqrt{25} \\[10pt] &= 5 \ \mathrm{[\Omega]} \end{aligned} \]次に、電流を計算します:
\[ \begin{eqnarray} I' &=& \frac{E'}{\sqrt{R_Y^2 + X_Y^2}} \\[20pt] &=& \frac{200}{\sqrt{4^2 + 3^2}} \\[20pt] &=& \frac{200}{5} \\[20pt] &=& 40 \ \mathrm{[A]} \end{eqnarray} \]したがって、線路を流れる電流は40[A]です。
ええ計算やな!最後に、全消費電力P'を求めてみよか。三相平衡負荷における全消費電力の求め方はどうやったっけ?
三相平衡負荷の全消費電力を計算します。
Y結線の場合、三相全体の消費電力は各相の消費電力の3倍となります。各相の消費電力は抵抗による損失なので、P = R·I²で計算できます。
\[ \begin{eqnarray} P' &=& 3R_Y {I'}^2 \\[20pt] &=& 3 \times 4 \times 40^2 \\[20pt] &=& 3 \times 4 \times 1600 \\[20pt] &=& 12 \times 1600 \\[20pt] &=& 19200 \ \mathrm{[W]} \\[20pt] &=& 19.2 \ \mathrm{[kW]} \end{eqnarray} \]したがって、全消費電力は19.2[kW]です。
これで問題(b)の答えは選択肢の(4)となります。
素晴らしい計算やな!これで問題(b)の答えが選択肢(4)の19.2[kW]と確認できました。
今回の問題のポイントをまとめておこか:
1. Y結線では相電圧 = 線間電圧÷√3、相電流 = 線電流
2. 力率からインピーダンスの抵抗成分とリアクタンス成分を求める方法:
\[ \begin{aligned} R &= Z \cdot \cos\theta \\[10pt] X &= Z \cdot \sin\theta = Z \cdot \sqrt{1 - \cos^2\theta} \\[10pt] Z_Y &= \dfrac{Z_\Delta}{3} \end{aligned} \]
4. 三相平衡負荷の全消費電力: P = 3·R·I²
これらの関係式は三相回路を解く上で重要やから、しっかり覚えておいてな!理解できたかな?
はい、理解できました!まとめていただいたポイントはとても分かりやすいです。
特に重要なのは:
・Y結線とΔ結線の特性の違い
・力率からインピーダンスの成分を求める方法
・Δ-Y変換の式
・三相平衡負荷の消費電力の計算方法
これらは電気主任技術者試験でも頻出の内容なので、きちんと覚えておきます。問題(a)の答えが選択肢(3)の9[Ω]、問題(b)の答えが選択肢(4)の19.2[kW]であることも確認できました。
三相回路の計算は、適切な変換と関係式を用いることで効率的に解けることがよくわかりました。ありがとうございました!
ええやん!三相回路の計算はちょっと複雑に見えるかもしれんけど、基本的な関係式を覚えておけば解けるようになるで。
実際の電力系統や工場の電気設備でもこういう三相回路の知識は必須やから、しっかり身につけてな。特に力率改善のための設備設計なんかでは、今日学んだ計算がそのまま使われるんやで。
これからも頑張っていこか!今日はお疲れさん!
はい、ありがとうございました先生!
三相回路の基本的な関係式をしっかり覚えておきます。実際の電力系統や工場設備でも使われる重要な知識だとわかり、より身が入りました。特に力率改善の設備設計にも応用できるということで、実務的な価値も理解できました。
Y結線とΔ結線の変換や、力率を考慮したインピーダンス計算など、今日学んだことを確実に身につけて、次回の学習にも活かしていきたいと思います。今日もありがとうございました!
解説まとめ
■ 三相交流回路とΔ-Y変換
三相交流回路は電力系統において基本的な回路構成です。負荷の接続方式にはY結線(スター結線)とΔ結線(デルタ結線)があり、それぞれに特徴があります。これらの回路は計算を簡略化するためにΔ-Y変換(またはY-Δ変換)を行うことがあります。この変換により、複雑な回路を同等の特性を持つ別の形式に変換して解析することができます。
■ 計算手順と公式
- 相電圧と線間電圧の関係
三相交流のY結線において、相電圧と線間電圧の関係を理解します。
\( E = \frac{V_L}{\sqrt{3}} \)
ここで、Eは相電圧、VLは線間電圧です。
- インピーダンスと力率の関係
力率からインピーダンスの抵抗成分とリアクタンス成分を計算します。
\( R = Z \cos \theta \)
\( X = Z \sin \theta = Z \sqrt{1-\cos^2 \theta} \)
ここで、Rは抵抗、Xはリアクタンス、Zはインピーダンスの大きさ、cos θは力率です。
- Δ-Y変換
Δ結線の各素子をY結線の等価な素子に変換します。
\( R_Y = \frac{R}{3} \)
\( X_Y = \frac{X}{3} \)
ここで、RYとXYはY結線に変換後の各相の抵抗とリアクタンスです。
- 電流と電力の計算
変換後の回路で電流と消費電力を計算します。
\( I = \frac{E}{\sqrt{R^2+X^2}} \)
\( P = 3RI^2 \)
ここで、Iは電流、Pは三相全体の消費電力です。
■ 具体的な計算例
問題条件
- (a) 三相交流回路、Y結線負荷
- 線間電圧: \( V_L = 210 \ \mathrm{[V]} \)
- 線電流: \( I = \frac{14}{\sqrt{3}} \ \mathrm{[A]} \)
- 力率: \( \cos \theta = 0.8 \)
- (b) 同じ負荷をΔ結線に変更
- 線間電圧: \( V_L' = 200 \ \mathrm{[V]} \)
(a) Y結線負荷のインピーダンスとリアクタンスの計算
\[ \begin{aligned} \text{相電圧の計算:} \\ E &= \frac{V_L}{\sqrt{3}} = \frac{210}{\sqrt{3}} \ \mathrm{[V]} \\[10pt] \text{負荷インピーダンスの計算:} \\ Z &= \frac{E}{I} = \frac{\frac{210}{\sqrt{3}}}{\frac{14}{\sqrt{3}}} \\[5pt] &= \frac{210}{14} \\[5pt] &= 15 \ \mathrm{[\Omega]} \\[10pt] \text{リアクタンスの計算:} \\ X &= Z \sin \theta = Z \sqrt{1-\cos^2 \theta} \\[5pt] &= 15 \times \sqrt{1-0.8^2} \\[5pt] &= 15 \times \sqrt{1-0.64} \\[5pt] &= 15 \times \sqrt{0.36} \\[5pt] &= 15 \times 0.6 \\[5pt] &= 9 \ \mathrm{[\Omega]} \end{aligned} \]結論:誘導性リアクタンスの大きさは 9 [Ω] である。(解答:選択肢(3))
(b) Δ結線に変更した場合の全消費電力の計算
\[ \begin{aligned} \text{抵抗値の計算:} \\ R &= Z \cos \theta \\[5pt] &= 15 \times 0.8 \\[5pt] &= 12 \ \mathrm{[\Omega]} \\[10pt] \text{Δ-Y変換:} \\ R_Y &= \frac{R}{3} = \frac{12}{3} = 4 \ \mathrm{[\Omega]} \\[5pt] X_Y &= \frac{X}{3} = \frac{9}{3} = 3 \ \mathrm{[\Omega]} \\[10pt] \text{線路電流の計算:} \\ I' &= \frac{E'}{\sqrt{R_Y^2+X_Y^2}} \\[5pt] &= \frac{200}{\sqrt{4^2+3^2}} \\[5pt] &= \frac{200}{\sqrt{16+9}} \\[5pt] &= \frac{200}{\sqrt{25}} \\[5pt] &= \frac{200}{5} \\[5pt] &= 40 \ \mathrm{[A]} \\[10pt] \text{全消費電力の計算:} \\ P' &= 3R_Y {I'}^2 \\[5pt] &= 3 \times 4 \times 40^2 \\[5pt] &= 3 \times 4 \times 1600 \\[5pt] &= 12 \times 1600 \\[5pt] &= 19200 \ \mathrm{[W]} \\[5pt] &= 19.2 \ \mathrm{[kW]} \end{aligned} \]結論:全消費電力は 19.2 [kW] である。(解答:選択肢(4))
■ 実務上の留意点
三相交流回路とΔ-Y変換の理解は電気設備設計において重要です。
- 三相モータなどの大型機器では、始動時の突入電流を抑えるために、Y-Δ始動法が用いられることがあります。
- Δ結線は相電流が線電流の√3倍となるため、大電流が流れる場合の素子選定に注意が必要です。
- Y結線では中性点の接地方法によって、地絡事故時の保護方式が異なります。
- 実際の設備では、三相不平衡による中性線電流や高調波の影響も考慮する必要があります。
- Δ結線は循環電流が流れる可能性があるため、各相のインピーダンスのバランスが重要です。